Web3 解密 Uniswap V2：流动性添加与手续费源码剖析

Web3 浪潮下，Uniswap V2 作为 DeFi 的核心引擎，其流动性添加与手续费机制如何运作？本文将深入剖析 addLiquidity 函数与手续费计算的源码，结合数学推导与代码逻辑，解密 Uniswap V2 的技术内核。无论你是开发者还是 Web3 爱好者，这里有你想要的答案！

本文聚焦 Uniswap V2 的核心功能，通过源码逐层解析 addLiquidity 的流动性添加流程，从代币比例计算到 LP 代币铸造，揭示其背后的恒定乘积公式。同时，深入探讨手续费机制，推导费用分配逻辑并剖析代码实现。无论是 Web3 技术细节还是 DeFi 设计理念，本文为你一一解密，带来从理论到实践的全景式剖析。

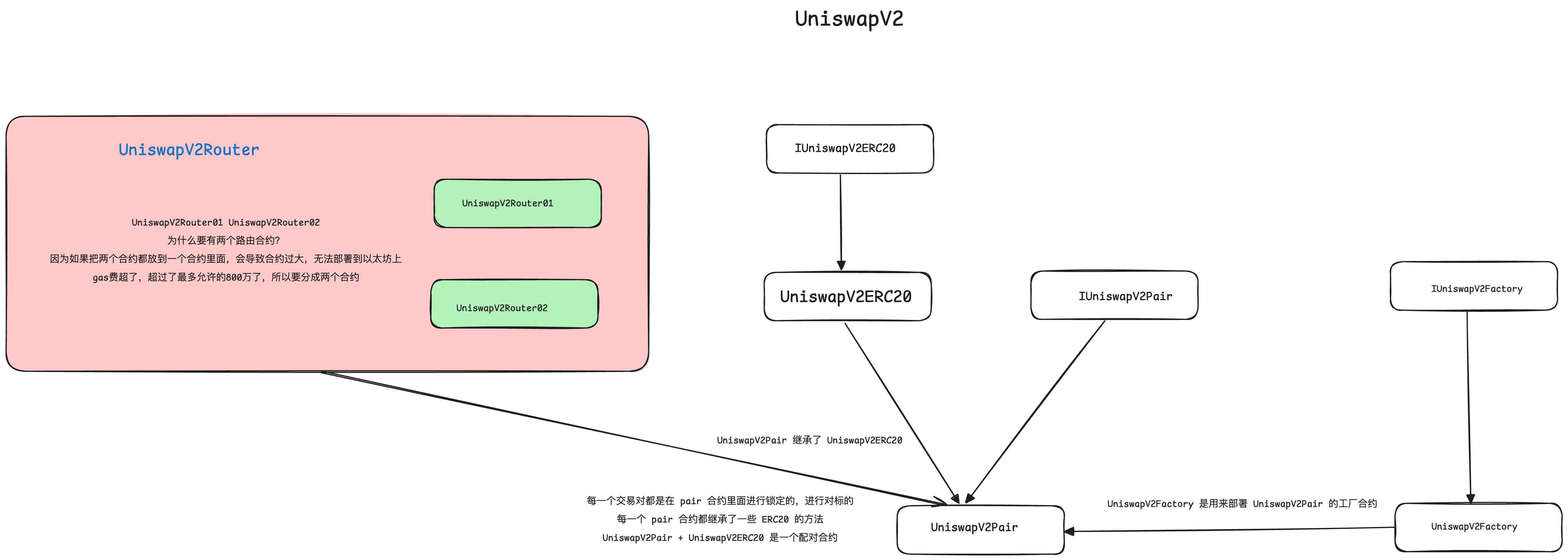
UniswapV2 添加流动性 addLiquidity 源码解析

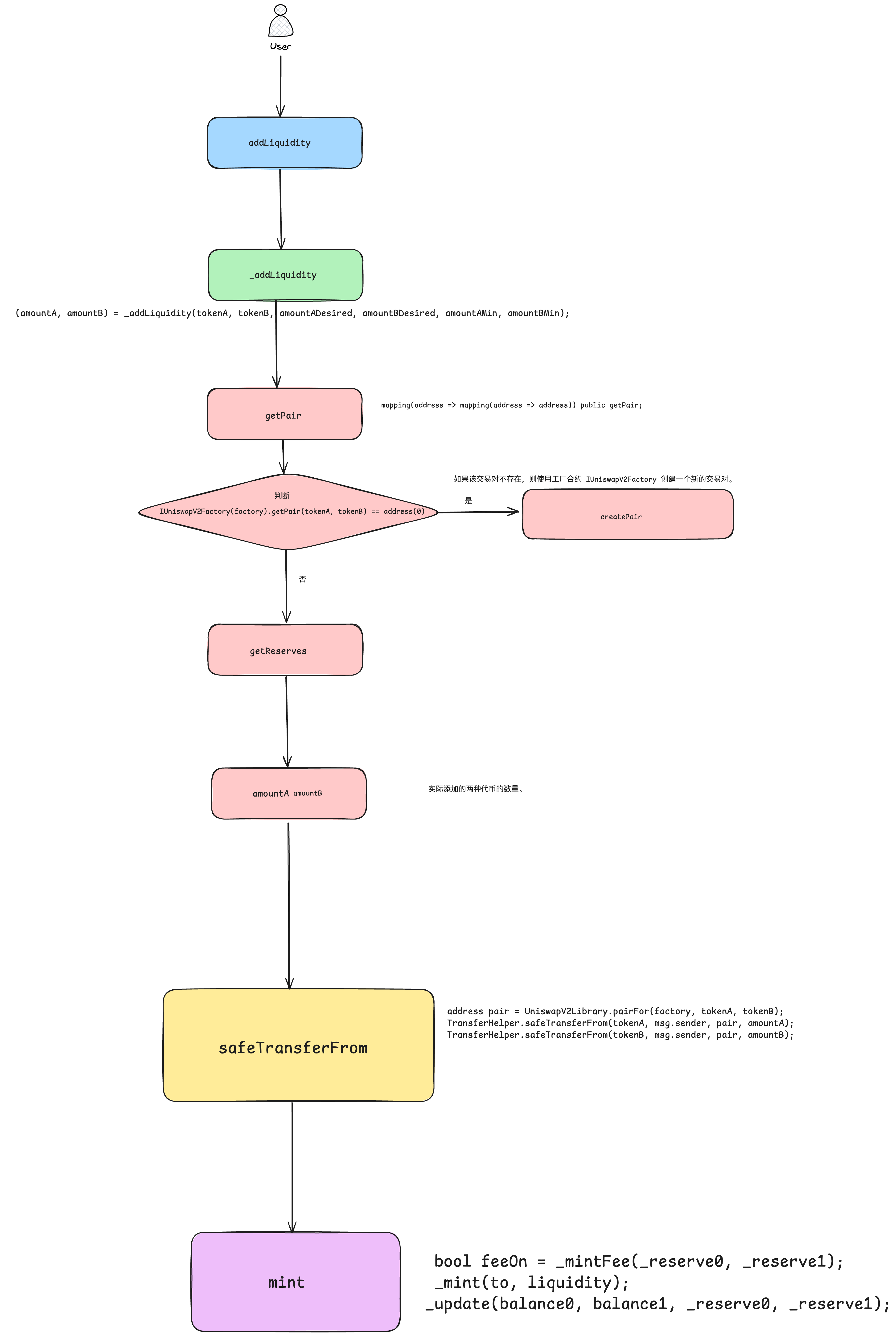
添加流动性 addLiquidity

用户在添加流动性的时候，用户首先调用 UniswapV2Router.sol 合约，提供 Token A 和 Token B 的数量，UniswapV2Router.sol 合约的 addLiquidity 函数接收用户的请求并进行处理。

 function addLiquidity(
        address tokenA,
        address tokenB,
        uint256 amountADesired,
        uint256 amountBDesired,
        uint256 amountAMin,
        uint256 amountBMin,
        address to,
        uint256 deadline
    ) external override ensure(deadline) returns (uint256 amountA, uint256 amountB, uint256 liquidity) {
        (amountA, amountB) = _addLiquidity(tokenA, tokenB, amountADesired, amountBDesired, amountAMin, amountBMin);
        address pair = UniswapV2Library.pairFor(factory, tokenA, tokenB);
        TransferHelper.safeTransferFrom(tokenA, msg.sender, pair, amountA);
        TransferHelper.safeTransferFrom(tokenB, msg.sender, pair, amountB);
        liquidity = IUniswapV2Pair(pair).mint(to);
    }

第一步：调用 _addLiquidity 函数来获取最终要添加的代币数量

// **** ADD LIQUIDITY ****
// tokenA, tokenB: 要添加流动性的两种代币的地址。
// amountADesired, amountBDesired: 希望添加的两种代币的数量。这是用户输入的参数，并非最终实际添加的数量。
// amountAMin, amountBMin: 两种代币的最小可接受数量。用于防止滑点过大。
// private: 该函数只能在合约内部调用。
// returns (uint256 amountA, uint256 amountB): 返回实际添加的两种代币的数量。
function _addLiquidity(
    address tokenA,
    address tokenB,
    uint256 amountADesired,
    uint256 amountBDesired,
    uint256 amountAMin,
    uint256 amountBMin
) private returns (uint256 amountA, uint256 amountB) {
    // 1. 创建交易对
    // 如果该交易对不存在，则使用工厂合约 IUniswapV2Factory 创建一个新的交易对。
    // create the pair if it doesn't exist yet
    if (IUniswapV2Factory(factory).getPair(tokenA, tokenB) == address(0)) {
        IUniswapV2Factory(factory).createPair(tokenA, tokenB);
    }
    // 2. 获取储备量
    // 从UniswapV2Library获取交易对中tokenA和tokenB的当前储备量。
    (uint256 reserveA, uint256 reserveB) = UniswapV2Library.getReserves(factory, tokenA, tokenB);
    // 3. 处理空储备量情况
    // 如果交易对是新创建的，储备量为0，则直接使用用户期望的添加量。
    if (reserveA == 0 && reserveB == 0) {
        (amountA, amountB) = (amountADesired, amountBDesired);
    } else {
        // 4. 计算最优添加量:
        // 否则，根据现有储备量和用户期望的amountADesired，使用UniswapV2Library.quote函数计算最优的amountB。
        // UniswapV2Library.quote 函数根据常数乘积公式计算，确保添加流动性后保持交易对的恒定乘积不变。
        // 用户希望添加的 amountADesired 和当前的储备量 reserveA 和 reserveB，计算出在保持恒定乘积的情况下，应该添加的 amountB 的最优值。
        // amountB = (amountADesired * reserveB) / reserveA
        uint256 amountBOptimal = UniswapV2Library.quote(amountADesired, reserveA, reserveB);
        // 5. 检查最小添加量:
        if (amountBOptimal <= amountBDesired) {
            // 检查计算出的amountB是否满足最小数量要求。如果不满足，则抛出异常。
            require(amountBOptimal >= amountBMin, "UniswapV2Router: INSUFFICIENT_B_AMOUNT");
            (amountA, amountB) = (amountADesired, amountBOptimal);
        } else {
            // 6. 处理amountBDesired小于最优amountB的情况
            //  amountAOptimal = (amountBDesired * reserveA) / reserveB;
            uint256 amountAOptimal = UniswapV2Library.quote(amountBDesired, reserveB, reserveA);
            assert(amountAOptimal <= amountADesired);
            require(amountAOptimal >= amountAMin, "UniswapV2Router: INSUFFICIENT_A_AMOUNT");
            // 通过计算 amountBOptimal 和 amountAOptimal，合约能够根据当前的流动性池状态和用户的输入，智能地决定应该添加多少代币，以保持流动性池的稳定性和有效性。
            // 这对于去中心化交易所（如 Uniswap）来说是非常重要的，因为它们依赖于流动性池的平衡来提供有效的交易价格和减少滑点。
            (amountA, amountB) = (amountAOptimal, amountBDesired);
        }
    }
}

在_addLiquidity 函数中，首先会根据 TokenA 、TokenB 通过 getPair 来查看交易对是否存在，如果不存在则通过 createPair 来创建。

mapping(address => mapping(address => address)) public getPair;



function createPair(address tokenA, address tokenB) external returns (address pair) {
    require(tokenA != tokenB, "UniswapV2: IDENTICAL_ADDRESSES");

    (address token0, address token1) = tokenA < tokenB ? (tokenA, tokenB) : (tokenB, tokenA);
    require(token0 != address(0), "UniswapV2: ZERO_ADDRESS");
    require(getPair[token0][token1] == address(0), "UniswapV2: PAIR_EXISTS"); // single check is sufficient
    //  用于获取 UniswapV2Pair 合约的创建字节码。这是一个智能合约编译器生成的字节码，用于在部署合约时初始化合约的代码。
    bytes memory bytecode = type(UniswapV2Pair).creationCode;
    bytes32 hash = keccak256(abi.encodePacked(bytecode));
    console.logBytes32("hash: ");
    console.logBytes32(hash);
    bytes32 salt = keccak256(abi.encodePacked(token0, token1));
    // CREATE2 是以太坊虚拟机 (EVM) 引入的一个 opcode，用于在智能合约中创建新合约。
    // 与传统的 CREATE opcode 不同，CREATE2 允许合约部署者在合约创建时指定合约地址，这样就可以预先知道新合约的地址。
    // CREATE2 是在以太坊硬分叉 Istanbul (EIP-1014) 中引入的。
    assembly {
        pair := create2(0, add(bytecode, 32), mload(bytecode), salt)
    }
    IUniswapV2Pair(pair).initialize(token0, token1);
    getPair[token0][token1] = pair;
    getPair[token1][token0] = pair; // populate mapping in the reverse direction
    allPairs.push(pair);
    emit PairCreated(token0, token1, pair, allPairs.length);
}

然后通过getReserves来获取对应的储备量

sortTokens 函数用于对两个代币地址进行排序，确保无论输入顺序如何，输出始终按照地址从小到大的顺序排列（即 token0 < token1）。

// returns sorted token addresses, used to handle return values from pairs sorted in this order
function sortTokens(address tokenA, address tokenB) internal pure returns (address token0, address token1) {
// 检查 tokenA 和 tokenB 是否相同，若相同则抛出错误（避免无效配对）
    require(tokenA != tokenB, "UniswapV2Library: IDENTICAL_ADDRESSES");
    (token0, token1) = tokenA < tokenB ? (tokenA, tokenB) : (tokenB, tokenA);
    require(token0 != address(0), "UniswapV2Library: ZERO_ADDRESS");
}


// calculates the CREATE2 address for a pair without making any external calls
function pairFor(address factory, address tokenA, address tokenB) internal pure returns (address pair) {
    (address token0, address token1) = sortTokens(tokenA, tokenB);
    bytes memory bytecode = type(UniswapV2Pair).creationCode;
    // bytes32 hash = keccak256(abi.encodePacked(bytecode));
    bytes32 hash = keccak256(
        abi.encodePacked(
            hex"ff", factory, keccak256(abi.encodePacked(token0, token1)), keccak256(abi.encodePacked(bytecode))
        )
    );
    // hex"7f88588ebc7bc61b03dfecb4cfa631fec5109b1a2b2ae99ccbf392424d7c5be1" // init code hash
    // 直接从 bytes32 类型转换为 address 类型
    pair = address(uint160(uint256(hash)));
}

// https://github.com/Uniswap/v2-periphery/blob/master/contracts/libraries/UniswapV2Library.sol
// fetches and sorts the reserves for a pair
function getReserves(address factory, address tokenA, address tokenB)
    internal
    view
    returns (uint256 reserveA, uint256 reserveB)
{
    (address token0,) = sortTokens(tokenA, tokenB); // 标准化代币地址顺序

    (uint256 reserve0, uint256 reserve1,) = IUniswapV2Pair(pairFor(factory, tokenA, tokenB)).getReserves();

    (reserveA, reserveB) = tokenA == token0 ? (reserve0, reserve1) : (reserve1, reserve0);
}

function getReserves() public view returns (uint112 _reserve0, uint112 _reserve1, uint32 _blockTimestampLast) {
      _reserve0 = reserve0;
      _reserve1 = reserve1;
      _blockTimestampLast = blockTimestampLast;
  }

如果交易对是新创建的，储备量为0，则直接使用用户期望的添加量。

 if (reserveA == 0 && reserveB == 0) {
            (amountA, amountB) = (amountADesired, amountBDesired);

否则，计算最优添加量:

根据现有储备量和用户期望的amountADesired，使用UniswapV2Library.quote函数计算最优的amountB

UniswapV2Library.quote 函数根据常数乘积公式计算，确保添加流动性后保持交易对的恒定乘积不变。

用户希望添加的 amountADesired 和当前的储备量 reserveA 和 reserveB，计算出在保持恒定乘积的情况下，应该添加的 amountB 的最优值。 $$ amountB = \frac{(amountADesired * reserveB) }{reserveA} $$

uint256 amountBOptimal = UniswapV2Library.quote(amountADesired, reserveA, reserveB);


// given some amount of an asset and pair reserves, returns an equivalent amount of the other asset
function quote(uint256 amountA, uint256 reserveA, uint256 reserveB) internal pure returns (uint256 amountB) {
    require(amountA > 0, "UniswapV2Library: INSUFFICIENT_AMOUNT");
    require(reserveA > 0 && reserveB > 0, "UniswapV2Library: INSUFFICIENT_LIQUIDITY");
    amountB = (amountA * reserveB) / reserveA;
}

恒定乘积公式

$$ x \cdot y = k = L^2 \ p = \frac{y}{x} \ $$ $$ \begin{align} L &= \sqrt{x \cdot y} \ &= \sqrt{x \cdot (p \cdot x)} \ &= \sqrt{x \cdot p \cdot x} \ &= \sqrt{x^2 \cdot p} \ &= x \cdot \sqrt{p} \end{align} $$

在代码中 $$ x \cdot y = k = L^2 \ $$ $$ reserveA \cdot reserveB = k = L^2 \ $$ $$ (x + \Delta x) \cdot (y + \Delta y) = k_1 \quad \text{其中} \quad k_1 > k \ $$

$$ (reserveA + amountA) \cdot (reserveB + amountB) = K1 $$ 添加流动性时，用户必须 按当前池中代币比例注入两种代币，以确保流动性池的价格比例（即 reserveA / reserveB）不变。这一约束条件可表示为： $$ \frac{\text{amountA}}{\text{amountB}} = \frac{\text{reserveA}}{\text{reserveB}} \tag{1} $$ 推导逻辑：

1. 原流动性池中代币储备为 reserveA 和 reserveB，满足 reserveA * reserveB = k = L²（L 为流动性总量）。

2. 用户注入 amountA 和 amountB 后，新储备量为 reserveA + amountA 和 reserveB + amountB。

3. 为确保注入后价格比例不变，需满足：

$$ \frac{\text{reserveA}}{\text{reserveB}} = \frac{\text{reserveA} + \text{amountA}}{\text{reserveB} + \text{amountB}} \tag{2} $$

公式推导

从约束条件式（2）出发： $$ \text{reserveA} \cdot (\text{reserveB} + \text{amountB}) = \text{reserveB} \cdot (\text{reserveA} + \text{amountA}) $$ 展开后： $$ \text{reserveA} \cdot \text{reserveB} + \text{reserveA} \cdot \text{amountB} = \text{reserveB} \cdot \text{reserveA} + \text{reserveB} \cdot \text{amountA} $$ 消去两边的 reserveA * reserveB 项： $$ \text{reserveA} \cdot \text{amountB} = \text{reserveB} \cdot \text{amountA} $$ 整理得： $$ \text{amountB} = \frac{\text{amountA} \cdot \text{reserveB}}{\text{reserveA}} $$

用户按比例注入代币后，流动性池规模扩大（k₁ > k），但价格比例保持不变。

在这里 amountB 也就是 amountBOptimal。

根据上面计算出的 amountBOptimal 和 用户期望添加的 amountBDesired 进行比较：

如果 amountBOptimal 小于等于 amountBDesired，则：

并且 amountBOptimal 大于等于 amountBMin

最终返回的 amountA = amountADesired，amountB = amountBOptimal

(amountA, amountB) = (amountADesired, amountBOptimal);

否则，计算amountAOptimal,计算过程与amountBOptimal一样，同上即可。 $$ \begin{align} \text{amountAOptimal} = \ \frac{\text{amountBDesired} \cdot \text{reserveA}}{\text{reserveB}} \end{align} $$ 通过计算 amountBOptimal 和 amountAOptimal，合约能够根据当前的流动性池状态和用户的输入，智能地决定应该添加多少代币，以保持流动性池的稳定性和有效性。

最终返回：

(amountA, amountB) = (amountAOptimal, amountBDesired);

到此为止，通过_addLiquidity函数可得到用户最终实际添加的两种代币的数量。即，

(amountA, amountB) = _addLiquidity(tokenA, tokenB, amountADesired, amountBDesired, amountAMin, amountBMin);

第二步：获取 pair 合约地址

address public immutable override factory;

address pair = UniswapV2Library.pairFor(factory, tokenA, tokenB);

// calculates the CREATE2 address for a pair without making any external calls
function pairFor(address factory, address tokenA, address tokenB) internal pure returns (address pair) {
    (address token0, address token1) = sortTokens(tokenA, tokenB);
    bytes memory bytecode = type(UniswapV2Pair).creationCode;
    // bytes32 hash = keccak256(abi.encodePacked(bytecode));
    bytes32 hash = keccak256(
        abi.encodePacked(
            hex"ff", factory, keccak256(abi.encodePacked(token0, token1)), keccak256(abi.encodePacked(bytecode))
        )
    );
    // hex"7f88588ebc7bc61b03dfecb4cfa631fec5109b1a2b2ae99ccbf392424d7c5be1" // init code hash
    // 直接从 bytes32 类型转换为 address 类型
    pair = address(uint160(uint256(hash)));
}

根据工厂合约地址、tokenA地址、tokenB地址通过pairFor 函数来计算出一个 CREATE2 address 作为交易对的合约地址。

第三步：Transfer Token

TransferHelper.safeTransferFrom(tokenA, msg.sender, pair, amountA);
TransferHelper.safeTransferFrom(tokenB, msg.sender, pair, amountB);

这段代码调用了TransferHelper合约中的safeTransferFrom函数，该函数用于从调用者账户（msg.sender）向指定的代币交换对（pair）转移代币

第四步：铸造流动性代币

addLiquidity 函数进一步调用 UniswapV2Pair.sol 合约，在 UniswapV2Pair.sol 合约中，调用 mint 函数执行实际的流动性添加操作，mint 函数根据用户提供的 Token A 和 Token B 的数量，计算应铸造的流动性代币（LP 代币）的数量，并将这些 LP 代币分配给用户，流动性添加操作完成后，mint 函数调用 _update 函数更新储备量。

liquidity = IUniswapV2Pair(pair).mint(to);

IUniswapV2Pair(pair)表示调用Uniswap V2交易对合约的接口。pair是一个合约地址，指向一个具体的Uniswap V2交易对合约。

mint(to)是Uniswap V2交易对合约中的一个函数，用于铸造新的流动性代币。to参数指定了新铸造的流动性代币接收者的地址。

流动性提供者通过提供一定数量的代币（通常是两种不同代币）来铸造流动性代币，这些代币代表了提供者的份额。流动性提供者可以通过这些流动性代币从交易对中赚取交易手续费。

pair是一个Uniswap V2交易对的合约地址，to是流动性代币接收者的地址，这段代码的作用就是通过调用Uniswap V2交易对合约的mint函数，铸造新的流动性代币，并将其发送到to地址。

// this low-level function should be called from a contract which performs important safety checks
function mint(address to) external lock returns (uint256 liquidity) {
    (uint112 _reserve0, uint112 _reserve1,) = getReserves(); // gas savings
    uint256 balance0 = IERC20(token0).balanceOf(address(this));
    uint256 balance1 = IERC20(token1).balanceOf(address(this));
    uint256 amount0 = balance0 - _reserve0;
    uint256 amount1 = balance1 - _reserve1;

    bool feeOn = _mintFee(_reserve0, _reserve1);
    uint256 _totalSupply = totalSupply; // gas savings, must be defined here since totalSupply can update in _mintFee
    if (_totalSupply == 0) {
        liquidity = Math.sqrt(amount0 * amount1) - MINIMUM_LIQUIDITY;
        _mint(address(0), MINIMUM_LIQUIDITY); // permanently lock the first MINIMUM_LIQUIDITY tokens
    } else {
        liquidity = Math.min((amount0 * _totalSupply) / _reserve0, (amount1 * _totalSupply) / _reserve1);
    }
    require(liquidity > 0, "UniswapV2: INSUFFICIENT_LIQUIDITY_MINTED");
    _mint(to, liquidity);

    _update(balance0, balance1, _reserve0, _reserve1);
    if (feeOn) kLast = reserve0 * reserve1; // reserve0 and reserve1 are up-to-date
    emit Mint(msg.sender, amount0, amount1);
}

这个函数的主要目的是在用户添加流动性时，铸造新的流动性代币并分配给提供流动性的用户。

1. 获取储备量：首先，函数通过调用getReserves()函数获取当前池子中两种代币（token0和token1）的储备量（_reserve0和_reserve1）。
2. 计算余额变化：接着，函数获取当前合约地址下两种代币的余额（balance0和balance1），并计算自上次更新以来两种代币的余额变化（amount0和amount1）。
3. 计算流动性：然后，函数根据余额变化和总供应量计算用户应获得的流动性代币数量。如果这是第一次添加流动性（即总供应量为0），则铸造的流动性代币数量减去一个固定的最小流动性值（MINIMUM_LIQUIDITY）。否则，根据余额变化和总储备量计算用户应得的流动性代币数量。

当 totalSupply 等于 0 的时候，即首次添加流动性，计算流动性如下：

 liquidity = Math.sqrt(amount0 * amount1) - MINIMUM_LIQUIDITY;

 uint256 public constant MINIMUM_LIQUIDITY = 10 ** 3;

$$ x \cdot y = k = L^2 \ $$ $$ \begin{align*} \text{恒定乘积常数} \quad k &= x \cdot y \ \text{流动性参数} \quad L &= \sqrt{k} \ &= \sqrt{x \cdot y} \ &= \sqrt{amount0 \cdot amount1} \end{align*} $$

代码中实际上首次添加计算出流动性后会扣除1000 wei，扣除的 1000 wei 会被永久锁定以增强系统安全性。

当 totalSupply不 等于 0 的时候，即非首次添加流动性时计算用户应获得的 LP 代币数量。

计算流动性（liquidity）如下：

liquidity = Math.min((amount0 * _totalSupply) / _reserve0, (amount1 * _totalSupply) / _reserve1);

1. 输入参数：

• amount0：用户在交易对中添加的某种代币的数量。
• amount1：用户在交易对中添加的另一种代币的数量。
• _totalSupply：当前交易对的流动性代币（通常称为LP代币）的总供应量。
• _reserve0：交易对中某种代币的储备量。
• _reserve1：交易对中另一种代币的储备量。

2. 计算过程：

• 首先，计算用户添加的代币数量与当前储备量的比例，分别对应两种代币。
• 具体计算公式为：
  • liquidity0 = (amount0 * _totalSupply) / _reserve0
  • liquidity1 = (amount1 * _totalSupply) / _reserve1
• 然后，取这两个比例中的最小值，作为用户的流动性。

公式推导

$$ \begin{align*} x \cdot y = k = L^2 \ reserve0 \cdot reserve1 = totalSupply^2 \ 添加流动性（k 增大） \ 当用户按比例存入代币时，新的储备量为： \ x’ = x + Δx \ y’ = y + Δy \ \end{align*} $$

$$ \begin{align*} 池子变为：\ x’ = reserve0 + amount0 \ y’ = reserve1 + amount1 \ k’ = x’* y’ \ \frac{x}{y} = \frac{Δx}{Δy} \ \frac{reserve0}{reserve1} = \frac{amount0}{amount1} \ \frac{x + Δx}{y + Δy} \end{align*} $$

基于上面的前提，我们进行下面的推导： $$ \begin{align*} L0 &= \frac{amount0}{reserve0} \cdot totalSupply \ &= \frac{amount0 \cdot totalSupply}{reserve0} \ \end{align*} $$ $$ \begin{align*} L1 &= \frac{amount1}{reserve1} \cdot totalSupply \ &= \frac{amount1 \cdot totalSupply}{reserve1} \ \end{align*} $$ L0 是你加的 amount0 占池子原来 reserve0 的比例，能拿多少 LP 代币

L1 是你加的 amount1 占池子原来 reserve1 的比例，能拿多少 LP 代币

最后 Uniswap 会取小的那个（Math.min(L_0, L_1)），保证你加的钱比例跟池子一致。

取小的是为了让池子保持原来的比例，不让你的“乱加钱”搞乱价格。

计算出需要 Mint 的流动性数量后调用_mint 函数进行Mint 铸造 LPT。

function _mint(address to, uint256 value) internal {
    totalSupply = totalSupply.add(value);
    balanceOf[to] = balanceOf[to].add(value);
    emit Transfer(address(0), to, value);
}

uint256 public override totalSupply;
mapping(address => uint256) public balanceOf;

这个函数主要实现了三步：

• 增加总供应量
• 增加接收者的余额
• 触发事件

最后更新储备数据并记录事件

 // update reserves and, on the first call per block, price accumulators
function _update(uint256 balance0, uint256 balance1, uint112 _reserve0, uint112 _reserve1) private {
    require(
        // balance0 <= uint112(-1) && balance1 <= uint112(-1),
        // 使用 uint112 的最大值来替代 -1
        balance0 <= type(uint112).max && balance1 <= type(uint112).max,
        "UniswapV2: OVERFLOW"
    );
    uint32 blockTimestamp = uint32(block.timestamp % 2 ** 32);
    uint32 timeElapsed = blockTimestamp - blockTimestampLast; // overflow is desired
    if (timeElapsed > 0 && _reserve0 != 0 && _reserve1 != 0) {
        // * never overflows, and + overflow is desired
        // _reserve1 * 2 ** 112 / _reserve0 * timeElapsed
        // 在 OraclePrice 使用，在本合约中只记录未使用
        // https://github.com/Uniswap/v2-periphery/blob/master/contracts/examples/ExampleOracleSimple.sol
        price0CumulativeLast += uint256(UQ112x112.encode(_reserve1).uqdiv(_reserve0)) * timeElapsed;
        price1CumulativeLast += uint256(UQ112x112.encode(_reserve0).uqdiv(_reserve1)) * timeElapsed;
    }
    reserve0 = uint112(balance0);
    reserve1 = uint112(balance1);
    blockTimestampLast = blockTimestamp;
    emit Sync(reserve0, reserve1);
}

记录事件

 emit Mint(msg.sender, amount0, amount1);

添加流动性完成！

Uniswap V2 的手续费

CPAMM

$$ x \cdot y = k = L^2 $$

$$ p = \frac{y}{x} $$

$$ L = \sqrt{x \cdot y} $$

$$ \begin{align} L &= \sqrt{x \cdot (p \cdot x)} \ &= \sqrt{x \cdot p \cdot x} \ &= \sqrt{x^2 \cdot p} \ &= x \cdot \sqrt{p} \end{align} $$

Uniswap V2 的手续费计算

1. 通过增发 share 的方式把手续费给项目方

$$ x \cdot y = k $$

$$ L = \sqrt{x \cdot y} = \sqrt{k} $$

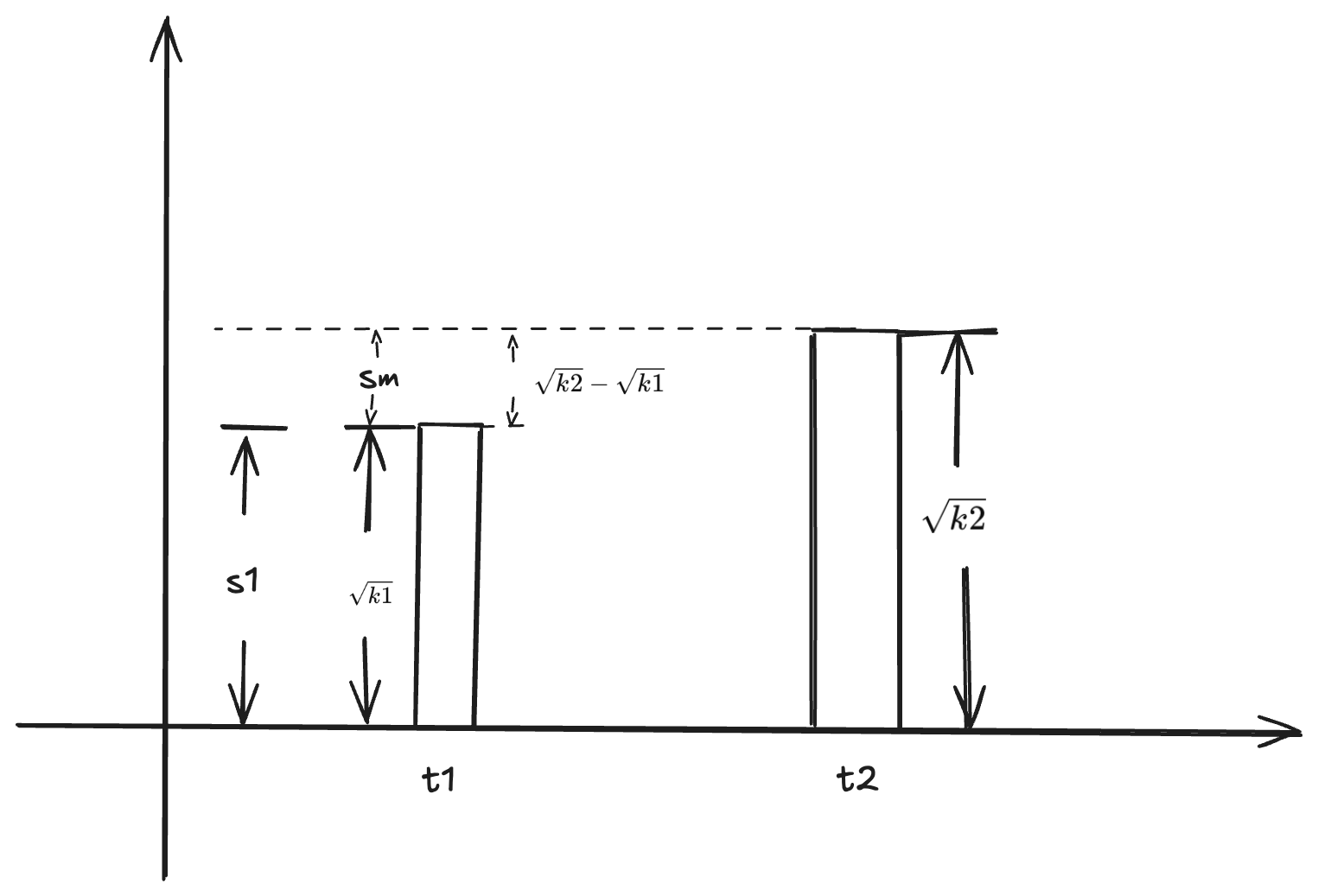$$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$

求 Sm

我们需要从方程

$$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$ 中解出 Sm。

解题步骤

1. 整理方程：

   从方程中我们可以得到： $$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$

2. 交叉相乘：

   将分数的两边交叉相乘，得到： $$ Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$

3. 展开右侧：

   展开右侧的括号：

$$ \begin{align} Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot Sm \

• (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align}

$$

4. 将 ( Sm ) 相关项移到一边：

   将含 ( Sm ) 的项移到方程的一侧：

$$ \begin{align} Sm \cdot \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) \cdot Sm \ = (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align} $$

5. 提取 ( Sm )：

   提取 ( Sm )：

$$ \begin{align} Sm \cdot (\sqrt{k2} - (\sqrt{k2} - \sqrt{k1})) \ = (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align} $$ 简化括号中的表达式： $$ \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) = \sqrt{k1} $$ 所以： $$ Sm \cdot \sqrt{k1} = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$

6. 解出 Sm ：

   通过除以$\sqrt{k1}$解出Sm：

   $$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$

最终结果

$$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$

2. 通过使 S1 增值的方式把手续费给 LP

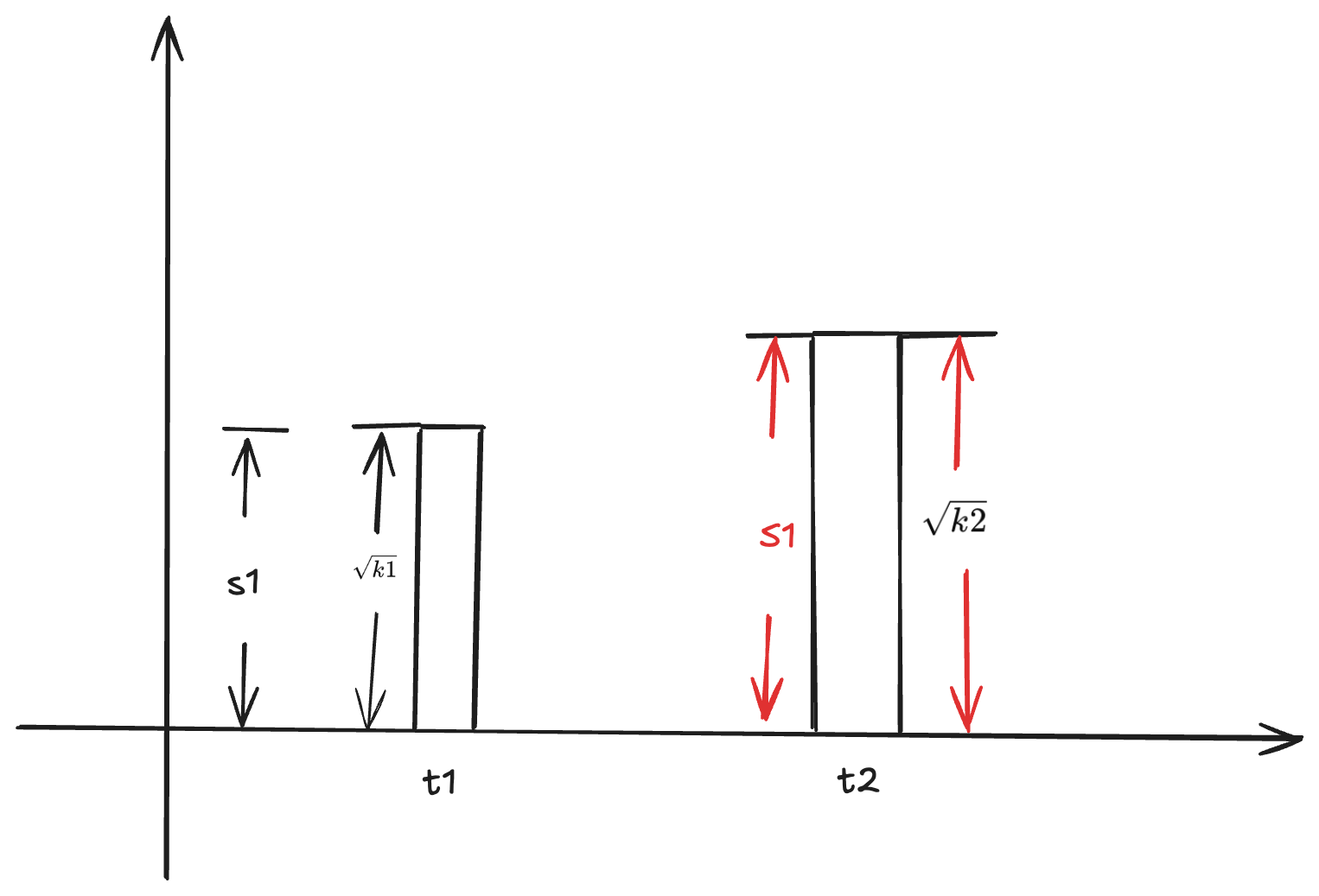
原来 S1 => $\sqrt{k1}$

现在 S1 = $\sqrt{k2}$

增值比例 $$ \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}} $$ LP Token

1 LPT => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ $\sqrt{k2}$ > $\sqrt{k1}$

1 LPT => 1 token A => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token A

1 LPT => 1 token B => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token B

3. 项目方想分走手续费里的一定比例，该比例用 $\Phi$ 表示

增值又增发

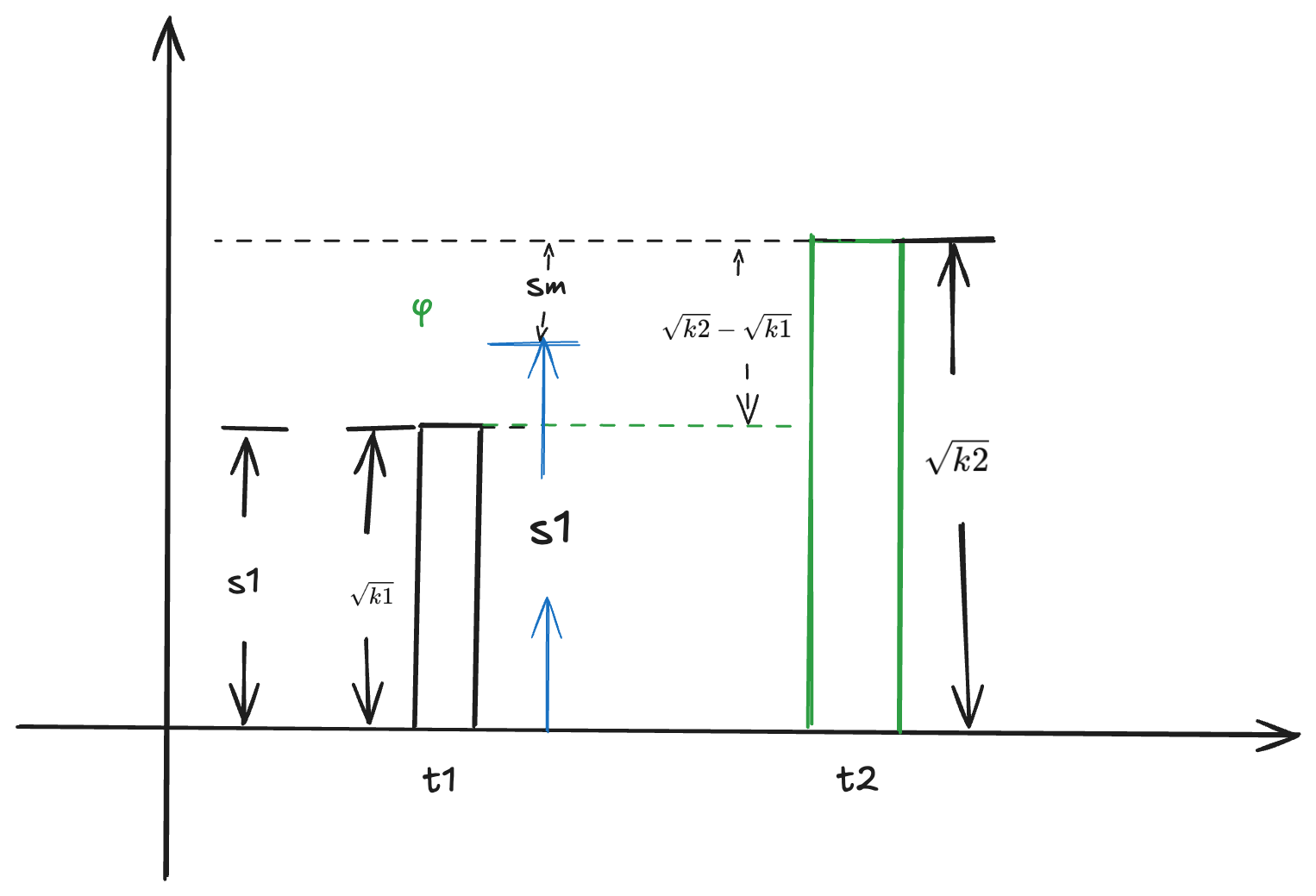
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$

求 Sm

我们通过以下步骤来推导：

原始公式

原始公式是：

$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$

交叉相乘

首先，将公式两边交叉相乘以消除分母：

$$ Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$

展开和重新排列

展开右侧的表达式：

$$ \begin{align} Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm \ + \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align} $$ 将包含 ( Sm ) 的项移到一边：

$$ \begin{align} Sm \cdot \sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm \ = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align} $$ 提取 ( Sm )：

$$ \begin{align} Sm \cdot \left(\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})\right) \ = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 \end{align} $$

简化

分母部分可以简化为：

$$ \sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 进一步简化为：

$$ \left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$

求解 ( Sm )

将分母形式替换回公式中，得到：

$$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}} $$

将分母部分进行化简

我们需要将分母部分调整成适当的形式。可以通过对分母进行重新表达来实现这一点：

$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 首先，我们从分母部分开始：

$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 为了将其变形为$ \frac{1}{\phi} - 1$ 的形式，我们可以使用以下变换：

1. 计算 $\frac{1}{\phi} - 1$:

这两个表达式相等的原因可以通过简单的代数变换来解释。我们将证明以下等式：

$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$

证明过程

1. 开始于左侧表达式:

   $$ \frac{1}{\phi} - 1 $$

2. 将 1 变成分母为 $\phi$的分数:

   我们知道 1 可以写成 $\frac{\phi}{\phi}$。因此，我们有：

   $$ \frac{1}{\phi} - 1 = \frac{1}{\phi} - \frac{\phi}{\phi} $$

3. 合并分数:

   为了合并这两个分数，我们需要它们具有相同的分母。现在它们都有分母 (\phi)，可以合并为一个分数：

   $$ \frac{1 - \phi}{\phi} $$

总结

通过代数变换，我们可以看到：

$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$ 这说明这两个表达式是相等的。 $$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$

将这个变换应用到分母中，得到：

$$ \begin{align} \frac{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\phi}\ \frac{(1 - \phi) \cdot \sqrt{k2}}{\phi} + \frac{\phi}{\phi} \cdot \sqrt{k1}\ \ \left(\frac{1 - \phi}{\phi}\right) \cdot \sqrt{k2} + \sqrt{k1} \end{align} $$

注意：整理后推导过程

从给定的公式推导

$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$ 以下是详细的推导过程：

1. 开始从等式：

   $$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$

2. 将分母统一：

   我们可以将分数两边的 ( Sm + S1 ) 移到右边：

   $$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} \cdot (Sm + S1) $$

3. 展开右边的表达式： $$ \begin{align} Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm}{\sqrt{k2}} \ + \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} \end{align} $$

4. 将含有 ( Sm ) 的项移到等式的一边：

   $$ \begin{align} Sm - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm}{\sqrt{k2}} \ = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} \end{align} $$

5. 合并 ( Sm ) 的项：

   $$ \begin{align} Sm \left(1 - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}}\right) \ = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} \end{align} $$

6. 简化分母： 第一步： $$ \begin{align} 1 - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} \ = \frac{\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} \end{align} $$ 第二步： $$ \begin{align} \frac{\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} \ = \frac{\sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} \end{align} $$ 第三步： $$ \begin{align} \frac{\sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} \ = \frac{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} \end{align} $$

7. 代入分母并进一步简化：

   将分母代入到 ( Sm ) 的公式中： $$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}} $$

8. 将分子分母同时除以$\phi$：

   $$ Sm = \frac{\frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\phi}}{\frac{\left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\phi}} $$ 然后我们将分子分母约去$\phi$得到目标公式： $$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$

因此，通过上述推导，我们可以得出目标公式。即最终公式是： $$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 这是正确的公式，可以用于计算 ( Sm )。 $$ \frac{\sqrt{k2} - \sqrt{k1}}{(\frac{1}{\phi} - 1) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$

并求当 $\phi$ 等于$\frac{1}{6}$ 时，Sm 的表达式

当$ \phi = \frac{1}{6}$ 时，我们可以将 $\phi$代入公式进行求解。首先，将 $\phi = \frac{1}{6}$ 代入公式：

$$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 代入 $\phi = \frac{1}{6}$ 后，我们先计算 $\frac{1}{\phi}$：

$$ \frac{1}{\phi} = \frac{1}{\frac{1}{6}} = 6 $$ 然后计算 $\frac{1}{\phi} - 1$：

$$ \frac{1}{\phi} - 1 = 6 - 1 = 5 $$ 将这些值代入原公式中，我们得到：

$$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{5 \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 这是当$ \phi = \frac{1}{6}$ 时的 (Sm) 表达式。

这也就是 Uniswap V2 的手续费计算公式

更多详情可参考Uniswap V2 白皮书：https://uniswap.org/whitepaper.pdf

https://www.rareskills.io/post/uniswap-v2-mintfee

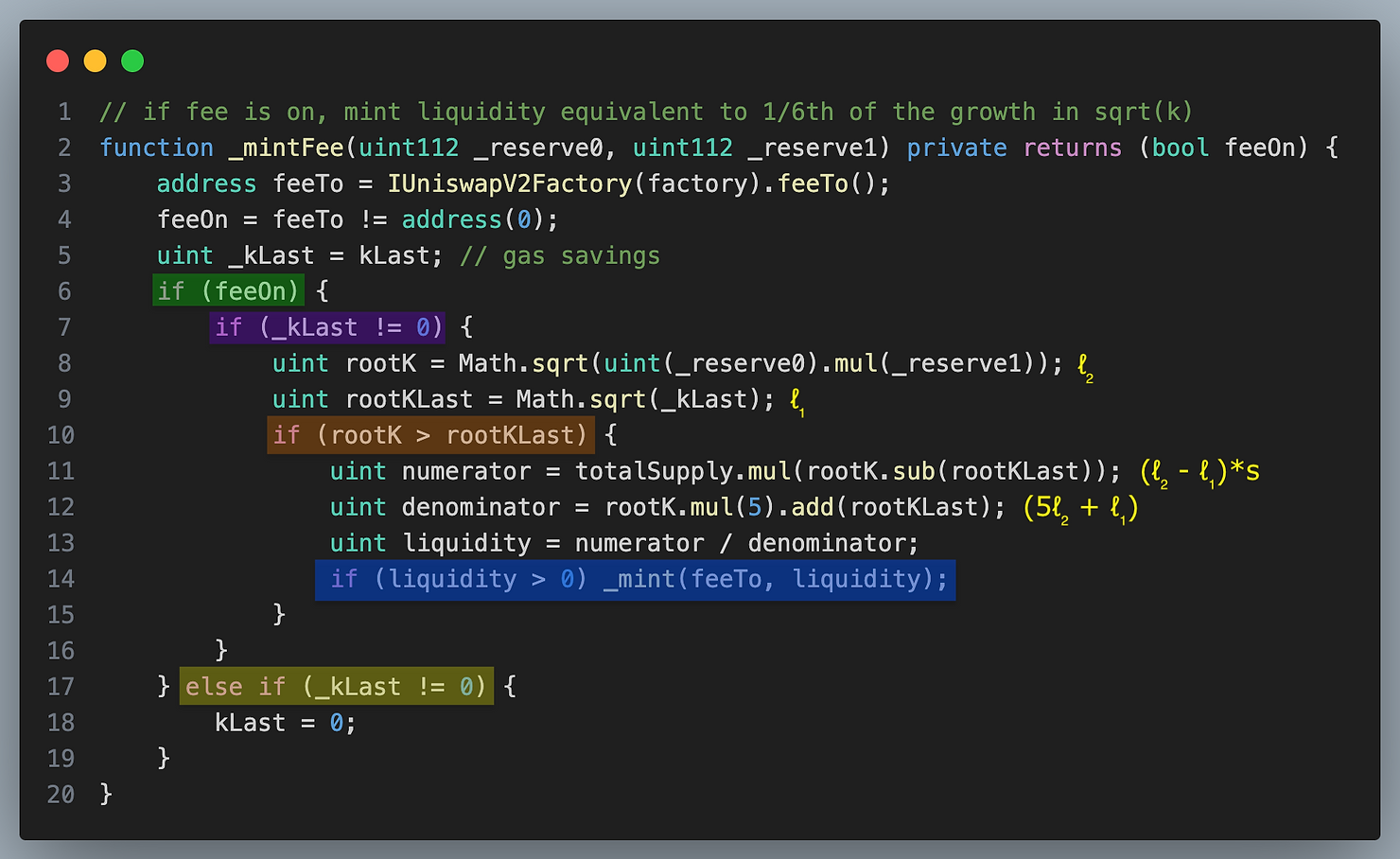
这是 Uniswap V2 源码对手续费的计算

https://github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Pair.sol

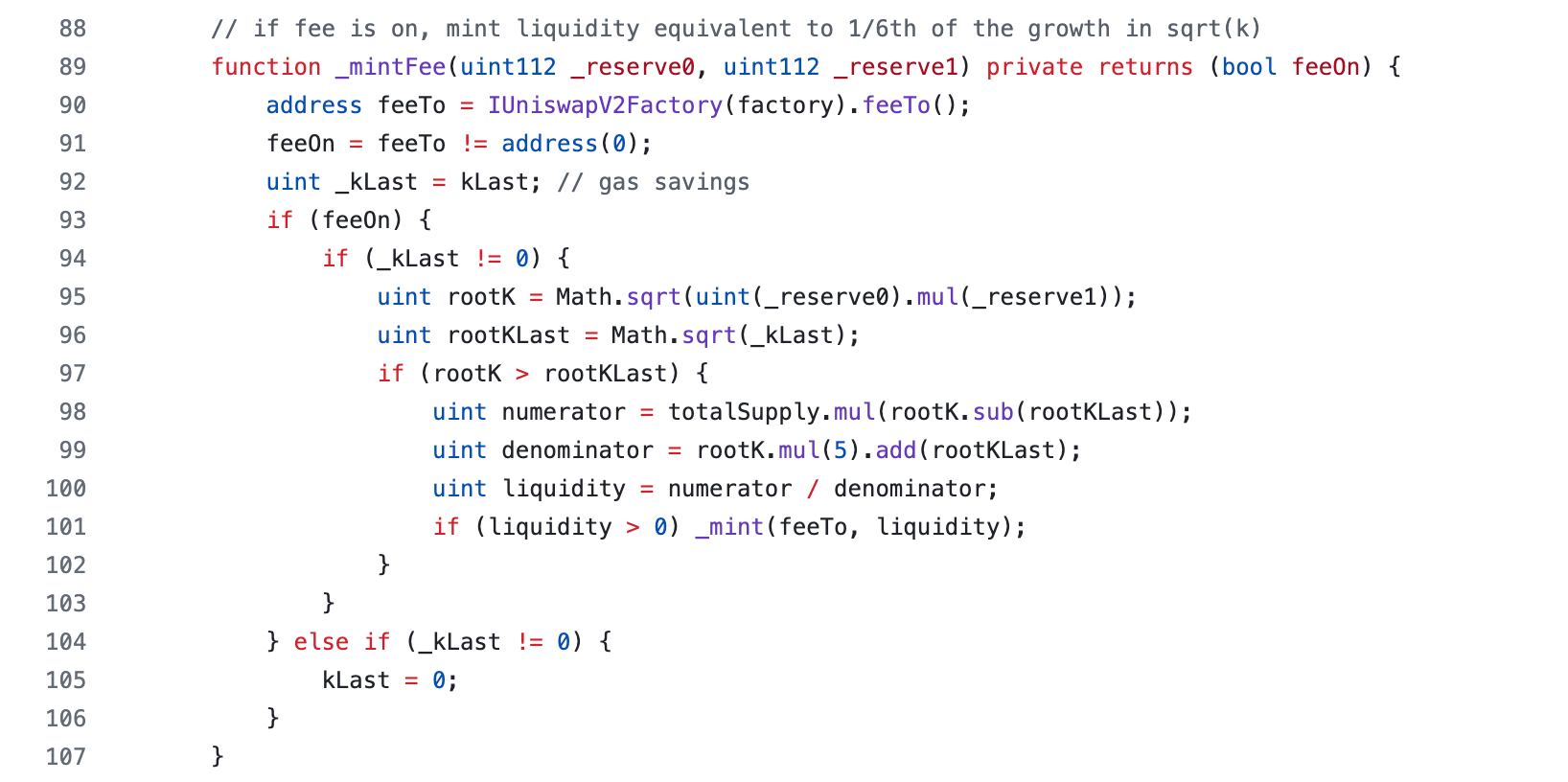
feeTo 是从工厂合约中获取的费用接收地址。如果地址不是零地址，则说明费用开启。

虽然函数中没有使用显式的 return 语句，feeOn 变量作为返回值在函数结尾处隐式返回。你可以依赖函数 _mintFee 的返回值来确定费用是否启用。

目前这个收手续费的开关是关闭的，其实是把所有的手续费给了 LP

这个手续费是在添加和移除流动性的时候收取

每次添加移除都会带来总量的mint或者是 burn

Uniswap V2 的设计目标是将 1/6 的手续费计入协议。由于手续费为 0.3%，其 1/6 为 0.05%，因此每笔交易的 0.05% 将计入协议。

因此，当流动性提供者调用burn 或 mint时，就会收取费用。由于这些操作与交换 token相比并不频繁，因此可以节省 gas。为了收取 mintFee ，合约会计算自上次发生以来收取的费用金额，并向受益人地址铸造足够的 LP 代币，以使受益人有权获得 1/6 的费用。

可以使用feeOn标志来开启或关闭费用,但是此功能从未真正启用过。

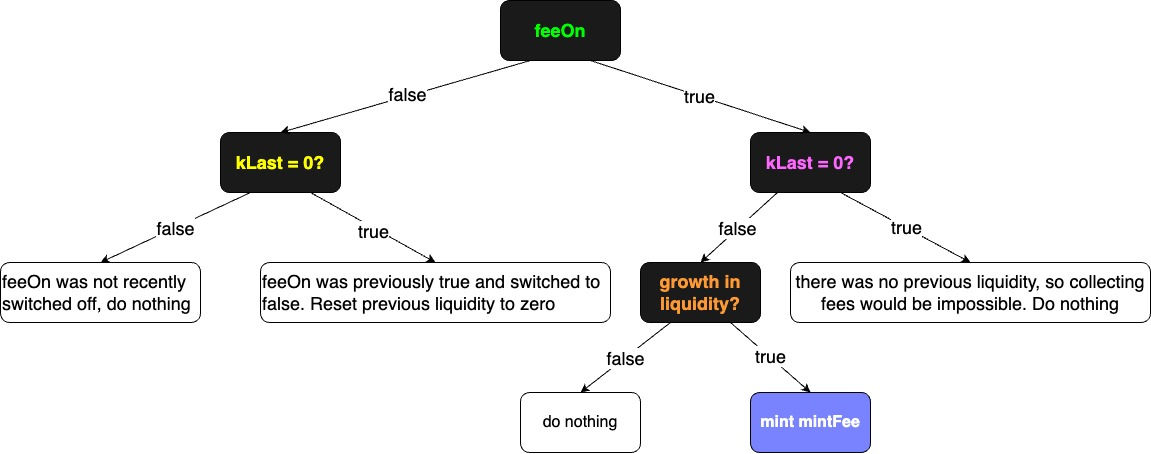
feeOn = feeTo != address(0);：如果 feeTo 不等于零地址 (address(0))，则 feeOn 为 true，表示启用了费用；否则，feeOn 为 false，表示费用未启用。

池子里钱咋动，k 咋变

大白话总结

• 交易：换来换去，k 不变，x/y 变。
• 加钱（添加流动性）：扔钱进去，x 和 y 变大，k 也变大。
• 拿钱（移除流动性）：拿走钱，x 和 y 变小，k 变小。

总结

Uniswap V2 在 Web3 生态中以其高效的流动性管理和手续费机制独树一帜。本文通过对 addLiquidity 函数和手续费计算的源码剖析，展示了其如何通过智能合约实现代币注入与费用分配。恒定乘积公式的应用确保了池子稳定性，而手续费设计则凸显了对 LP 的优先支持。从技术实现到数学原理，这场解密之旅为你揭开了 Uniswap V2 的核心奥秘。未完待续… 之后会继续分析移除流动性 removeLiquidity、Swap 等剩余源码，敬请期待！

参考

• https://github.com/Uniswap/v2-core
• https://github.com/Uniswap/v2-sdk
• https://github.com/Uniswap/foundry-template
• https://github.com/Uniswap/v2-periphery
• https://github.com/Uniswap/v2-subgraph
• https://thegraph.com/explorer
• https://app.uniswap.org/
• https://docs.uniswap.org/
• https://app.uniswap.org/whitepaper-v4.pdf
• https://docs.uniswap.org/contracts/v2/guides/smart-contract-integration/getting-pair-addresses
• https://www.rareskills.io/post/uniswap-v2-price-impact
• https://github.com/Dapp-Learning-DAO/Dapp-Learning/blob/main/defi/Uniswap-V2/readme.md
• https://github.com/qiaopengjun5162/V2-Core-08
• https://www.rareskills.io/post/uniswap-v2-mintfee
• https://www.coinbase.com/zh-cn/learn/crypto-basics/what-is-uniswap