Uniswap V2 的手续费计算
Table of Contents
Uniswap V2 的手续费计算
Uniswap V3 简介
- 2021年5月,Uniswap V3 发布
- 主要特性
- 增加集中流动性
- 优化手续费设置
- TWAP 优化
- 改进开源协议
Uniswap V2 的问题:资金利用效率(流动性)比较低或者说做LP风险很大
价格波动
V3 可以在一个价格波动范围内,而不是0到无穷
分层
V2 都是 千三 手续费 0.025 管理费 没打开
集中流动性
可以指定一个特定的价格段,即我在某个价格范围之内做流动性
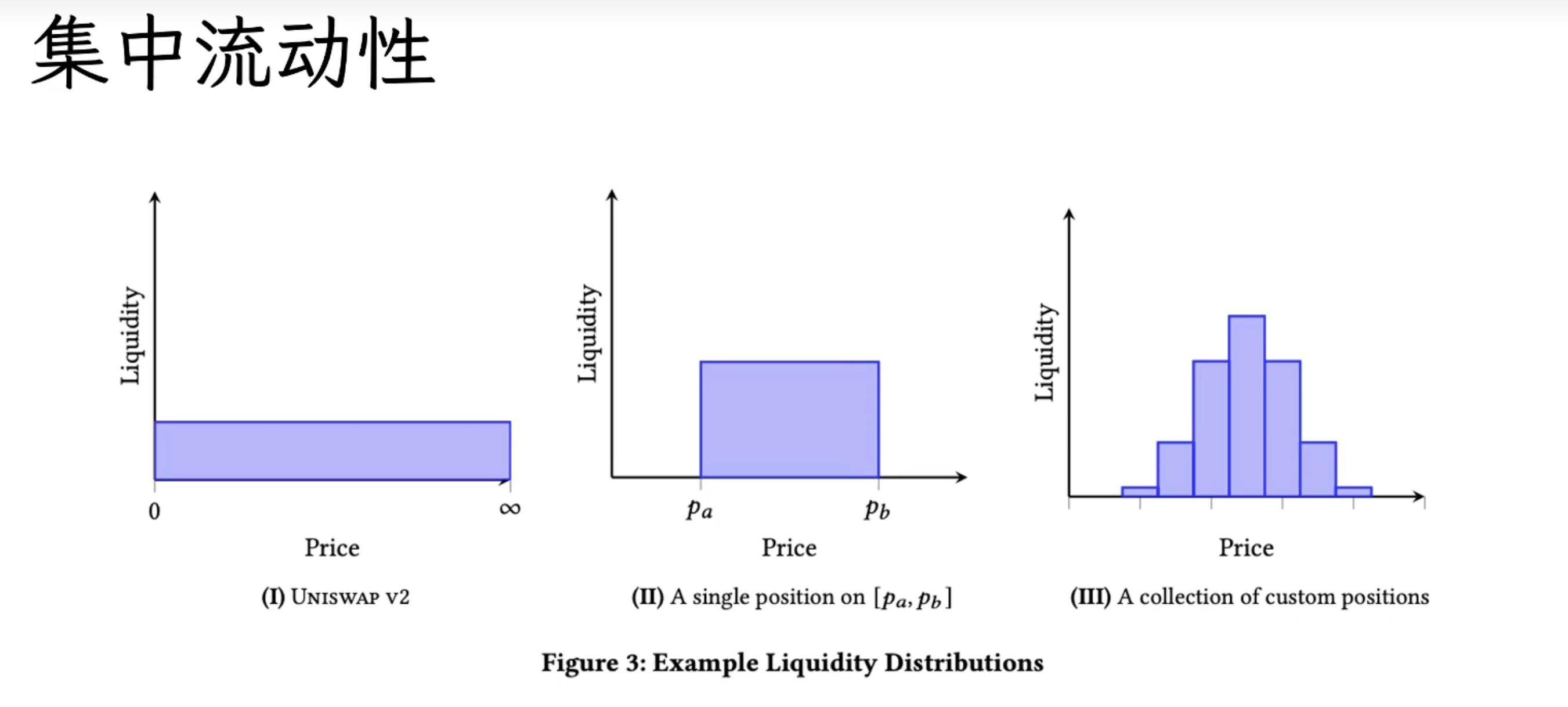
手续费
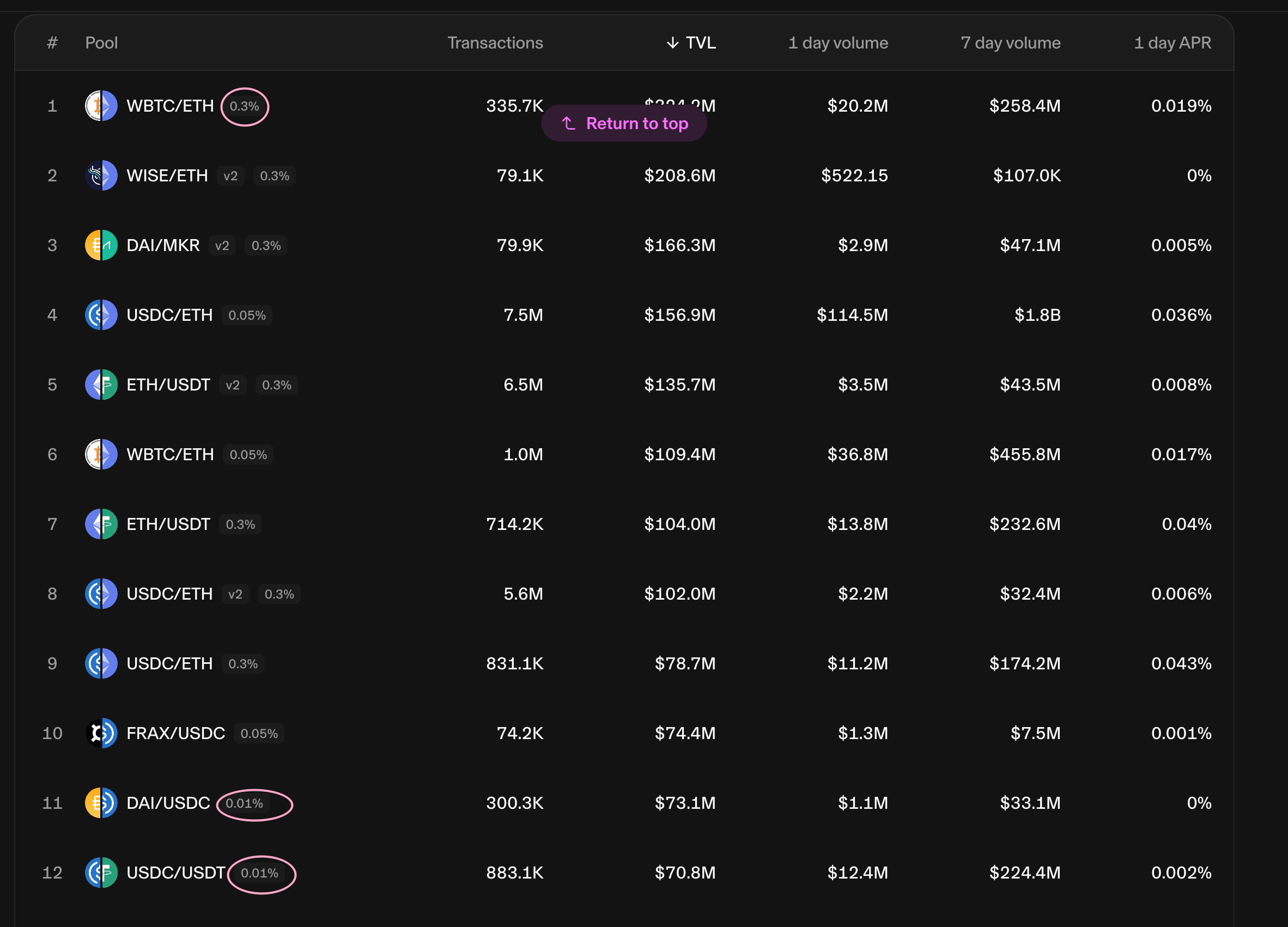
资金利用率的提升
Range Order
手续费收取
针对不同的交易对,收取不同的手续费,设置不同的梯度
0.01% 0.05% 0.30% 1.00%
管理费可以收取手续费的 10% ~ 25%
TWAP Oracle 改进
间隔时间记录
https://uniswap.org/whitepaper.pdf
Uniswap v3 Core 白皮书
https://uniswap.org/whitepaper-v3.pdf
如果只理解V3 一个事情的话,一定要理解虚拟流动性
通过设定一个价格范围,我只提供需要的流动性,达到的效果就和V2里面一样
Uniswap v3 的模拟器
https://www.desmos.com/calculator/6si0vmgwhc?lang=zh-CN
CPAMM
$$ x \cdot y = k = L^2 $$
$$ p = \frac{y}{x} $$
$$ L = \sqrt{x \cdot y} $$
$$ \begin{align} L &= \sqrt{x \cdot (p \cdot x)} \ &= \sqrt{x \cdot p \cdot x} \ &= \sqrt{x^2 \cdot p} \ &= x \cdot \sqrt{p} \end{align} $$
Uniswap V2 的手续费计算
1. 通过增发 share 的方式把手续费给项目方
$$ x \cdot y = k $$
$$ L = \sqrt{x \cdot y} = \sqrt{k} $$
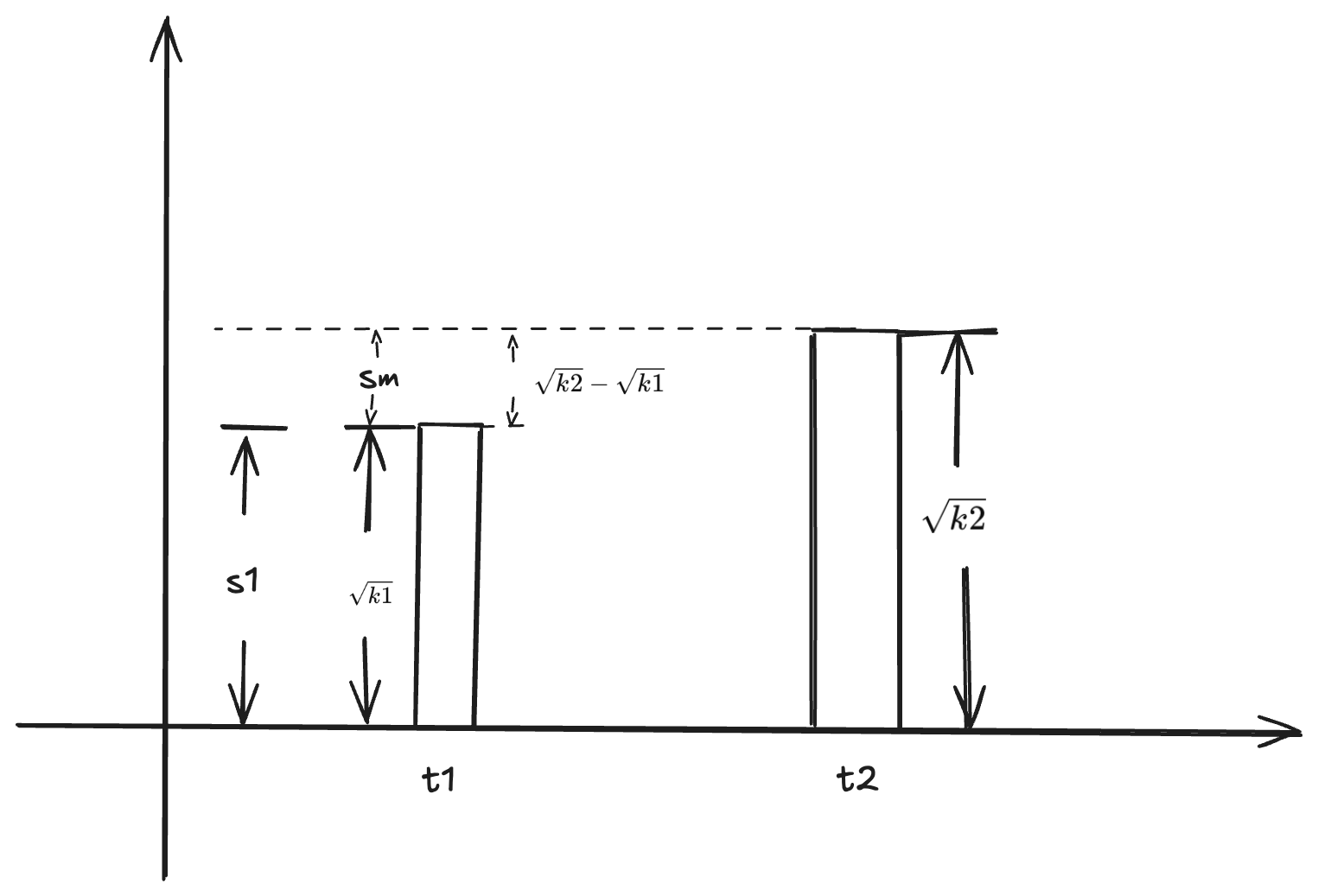 $$
\frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}}
$$
$$
\frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}}
$$
求 Sm
我们需要从方程
$$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$ 中解出 Sm。
解题步骤
-
整理方程:
从方程中我们可以得到: $$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$
-
交叉相乘:
将分数的两边交叉相乘,得到: $$ Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$
-
展开右侧:
展开右侧的括号: $$ Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot Sm + (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
将 ( Sm ) 相关项移到一边:
将含 ( Sm ) 的项移到方程的一侧: $$ Sm \cdot \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) \cdot Sm = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
提取 ( Sm ):
提取 ( Sm ): $$ Sm \cdot (\sqrt{k2} - (\sqrt{k2} - \sqrt{k1})) = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 简化括号中的表达式: $$ \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) = \sqrt{k1} $$ 所以: $$ Sm \cdot \sqrt{k1} = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
解出 Sm :
通过除以$\sqrt{k1}$解出Sm:
$$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$
最终结果
$$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$
2. 通过使 S1 增值的方式把手续费给 LP
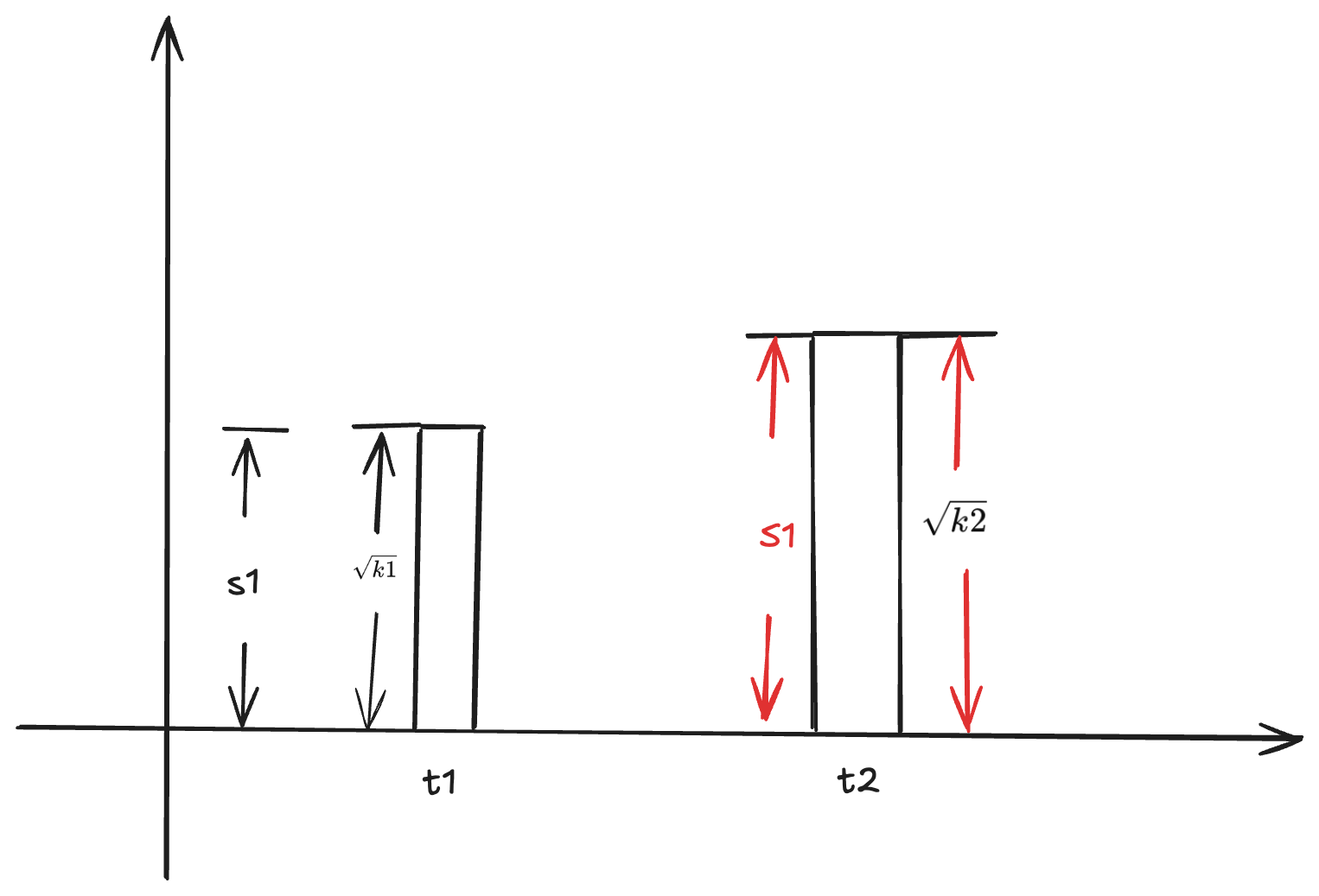
原来 S1 => $\sqrt{k1}$
现在 S1 = $\sqrt{k2}$
增值比例 $$ \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}} $$ LP Token
1 LPT => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ $\sqrt{k2}$ > $\sqrt{k1}$
1 LPT => 1 token A => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token A
1 LPT => 1 token B => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token B
3. 项目方想分走手续费里的一定比例,该比例用 $\Phi$ 表示
增值又增发
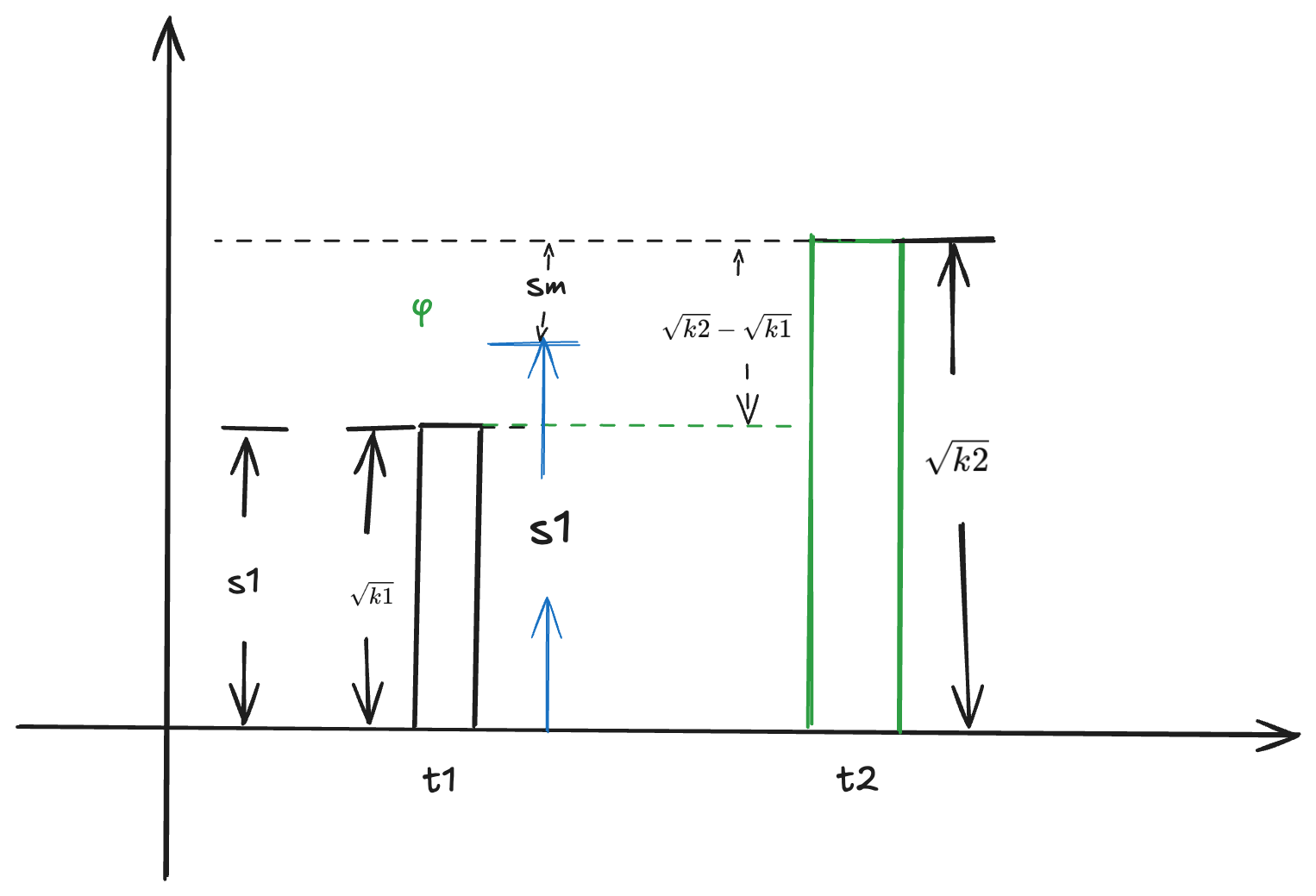
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$
求 Sm
我们通过以下步骤来推导:
原始公式
原始公式是:
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$
交叉相乘
首先,将公式两边交叉相乘以消除分母:
$$ Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$
展开和重新排列
展开右侧的表达式:
$$ Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm + \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 将包含 ( Sm ) 的项移到一边:
$$ Sm \cdot \sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 提取 ( Sm ):
$$ Sm \cdot \left(\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})\right) = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
简化
分母部分可以简化为:
$$ \sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 进一步简化为:
$$ \left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$
求解 ( Sm )
将分母形式替换回公式中,得到:
$$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}} $$
将分母部分进行化简
我们需要将分母部分调整成适当的形式。可以通过对分母进行重新表达来实现这一点:
$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 首先,我们从分母部分开始:
$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 为了将其变形为$ \frac{1}{\phi} - 1$ 的形式,我们可以使用以下变换:
- 计算 $\frac{1}{\phi} - 1$:
这两个表达式相等的原因可以通过简单的代数变换来解释。我们将证明以下等式:
$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$
证明过程
-
开始于左侧表达式:
$$ \frac{1}{\phi} - 1 $$
-
将 1 变成分母为 $\phi$的分数:
我们知道 1 可以写成 $\frac{\phi}{\phi}$。因此,我们有:
$$ \frac{1}{\phi} - 1 = \frac{1}{\phi} - \frac{\phi}{\phi} $$
-
合并分数:
为了合并这两个分数,我们需要它们具有相同的分母。现在它们都有分母 (\phi),可以合并为一个分数:
$$ \frac{1 - \phi}{\phi} $$
总结
通过代数变换,我们可以看到:
$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$ 这说明这两个表达式是相等的。 $$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$
将这个变换应用到分母中,得到:
$$ \frac{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\phi}\ \frac{(1 - \phi) \cdot \sqrt{k2}}{\phi} + \frac{\phi}{\phi} \cdot \sqrt{k1}\ \ \left(\frac{1 - \phi}{\phi}\right) \cdot \sqrt{k2} + \sqrt{k1} $$
注意:整理后推导过程
从给定的公式推导
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$ 以下是详细的推导过程:
-
开始从等式:
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$
-
将分母统一:
我们可以将分数两边的 ( Sm + S1 ) 移到右边:
$$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} \cdot (Sm + S1) $$
-
展开右边的表达式: $$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm}{\sqrt{k2}} + \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} $$
-
将含有 ( Sm ) 的项移到等式的一边:
$$ Sm - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm}{\sqrt{k2}} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} $$
-
合并 ( Sm ) 的项:
$$ Sm \left(1 - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}}\right) = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k2}} $$
-
简化分母: 第一步: $$ 1 - \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} = \frac{\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$ 第二步: $$ \frac{\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} = \frac{\sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} $$ 第三步: $$ \frac{\sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} = \frac{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\sqrt{k2}} $$
-
代入分母并进一步简化:
将分母代入到 ( Sm ) 的公式中: $$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{(1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}} $$
-
将分子分母同时除以$\phi$:
$$ Sm = \frac{\frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\phi}}{\frac{\left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}}{\phi}} $$ 然后我们将分子分母约去$\phi$得到目标公式: $$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$
因此,通过上述推导,我们可以得出目标公式。即最终公式是: $$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 这是正确的公式,可以用于计算 ( Sm )。 $$ \frac{\sqrt{k2} - \sqrt{k1}}{(\frac{1}{\phi} - 1) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$
并求当 $\phi$ 等于$\frac{1}{6}$ 时,Sm 的表达式
当$ \phi = \frac{1}{6}$ 时,我们可以将 $\phi$代入公式进行求解。首先,将 $\phi = \frac{1}{6}$ 代入公式:
$$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{\left(\frac{1}{\phi} - 1\right) \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 代入 $\phi = \frac{1}{6}$ 后,我们先计算 $\frac{1}{\phi}$:
$$ \frac{1}{\phi} = \frac{1}{\frac{1}{6}} = 6 $$ 然后计算 $\frac{1}{\phi} - 1$:
$$ \frac{1}{\phi} - 1 = 6 - 1 = 5 $$ 将这些值代入原公式中,我们得到:
$$ Sm = \frac{\sqrt{k2} - \sqrt{k1}}{5 \cdot \sqrt{k2} + \sqrt{k1}} \cdot S1 $$ 这是当$ \phi = \frac{1}{6}$ 时的 (Sm) 表达式。
这也就是 Uniswap V2 的手续费计算公式

更多详情可参考Uniswap V2 白皮书:https://uniswap.org/whitepaper.pdf
https://www.rareskills.io/post/uniswap-v2-mintfee
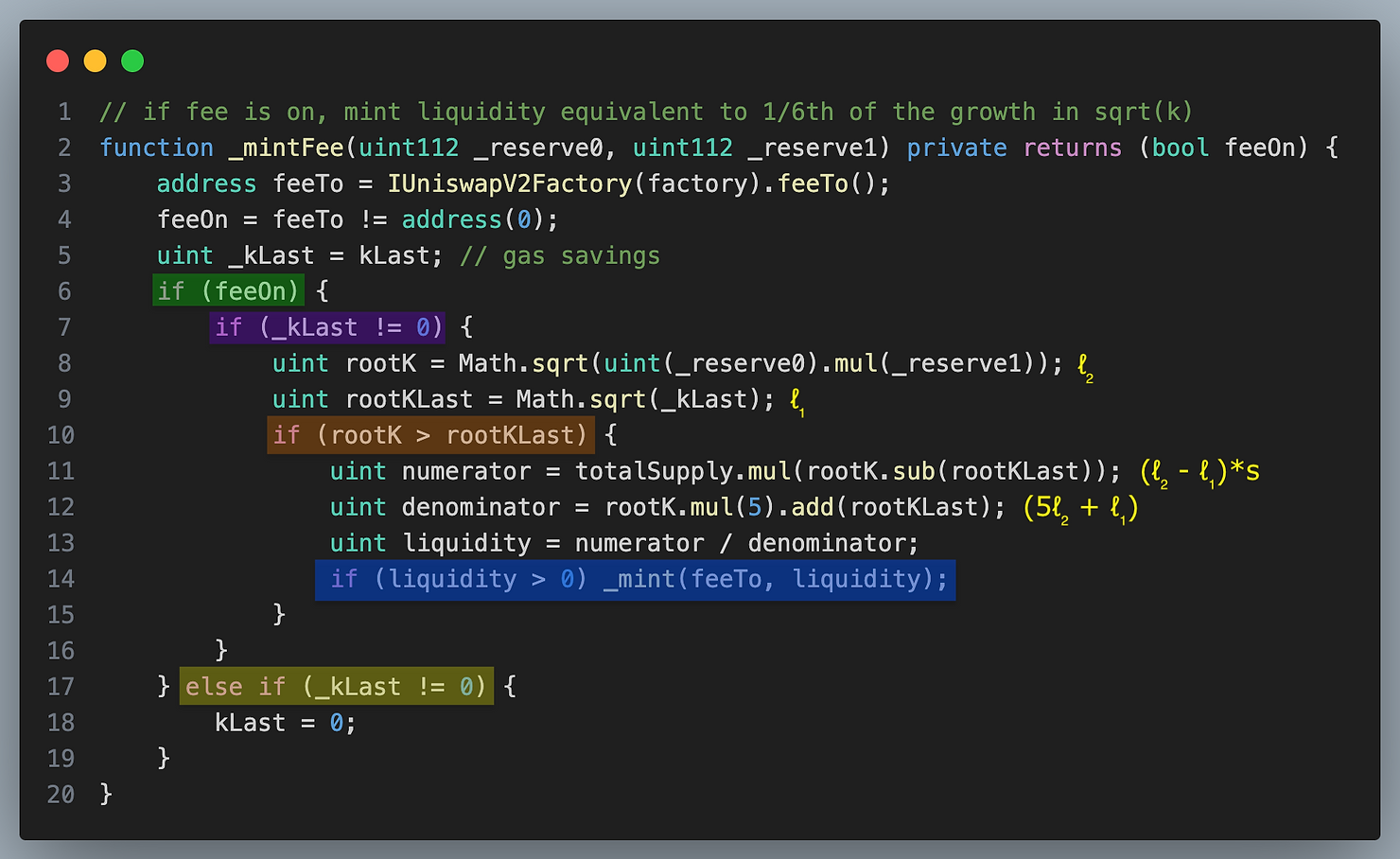
这是 Uniswap V2 源码对手续费的计算
https://github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Pair.sol
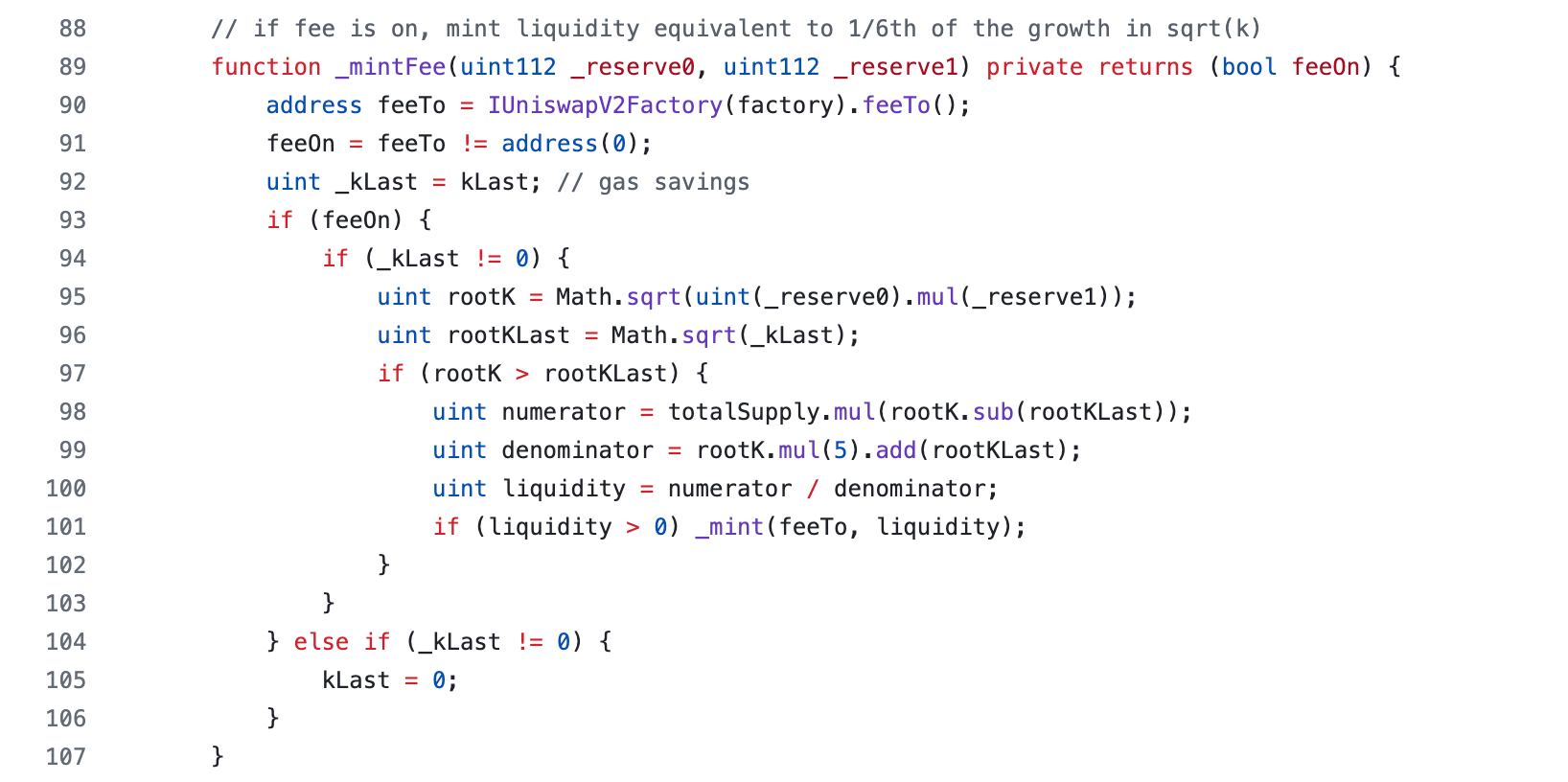
feeTo 是从工厂合约中获取的费用接收地址。如果地址不是零地址,则说明费用开启。
虽然函数中没有使用显式的 return 语句,feeOn 变量作为返回值在函数结尾处隐式返回。你可以依赖函数 _mintFee 的返回值来确定费用是否启用。
目前这个收手续费的开关是关闭的,其实是把所有的手续费给了 LP
这个手续费是在添加和移除流动性的时候收取
每次添加移除都会带来总量的mint或者是 burn

Uniswap V2 的设计目标是将 1/6 的手续费计入协议。由于手续费为 0.3%,其 1/6 为 0.05%,因此每笔交易的 0.05% 将计入协议。
因此,当流动性提供者调用burn 或 mint时,就会收取费用。由于这些操作与交换 token相比并不频繁,因此可以节省 gas。为了收取 mintFee ,合约会计算自上次发生以来收取的费用金额,并向受益人地址铸造足够的 LP 代币,以使受益人有权获得 1/6 的费用。
可以使用feeOn标志来开启或关闭费用,但是此功能从未真正启用过。
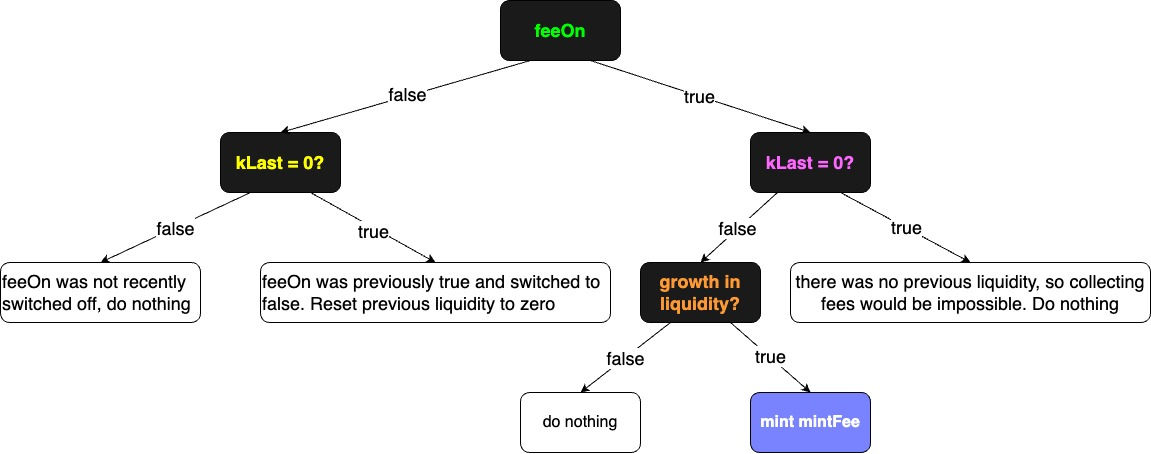
feeOn = feeTo != address(0);:如果 feeTo 不等于零地址 (address(0)),则 feeOn 为 true,表示启用了费用;否则,feeOn 为 false,表示费用未启用。